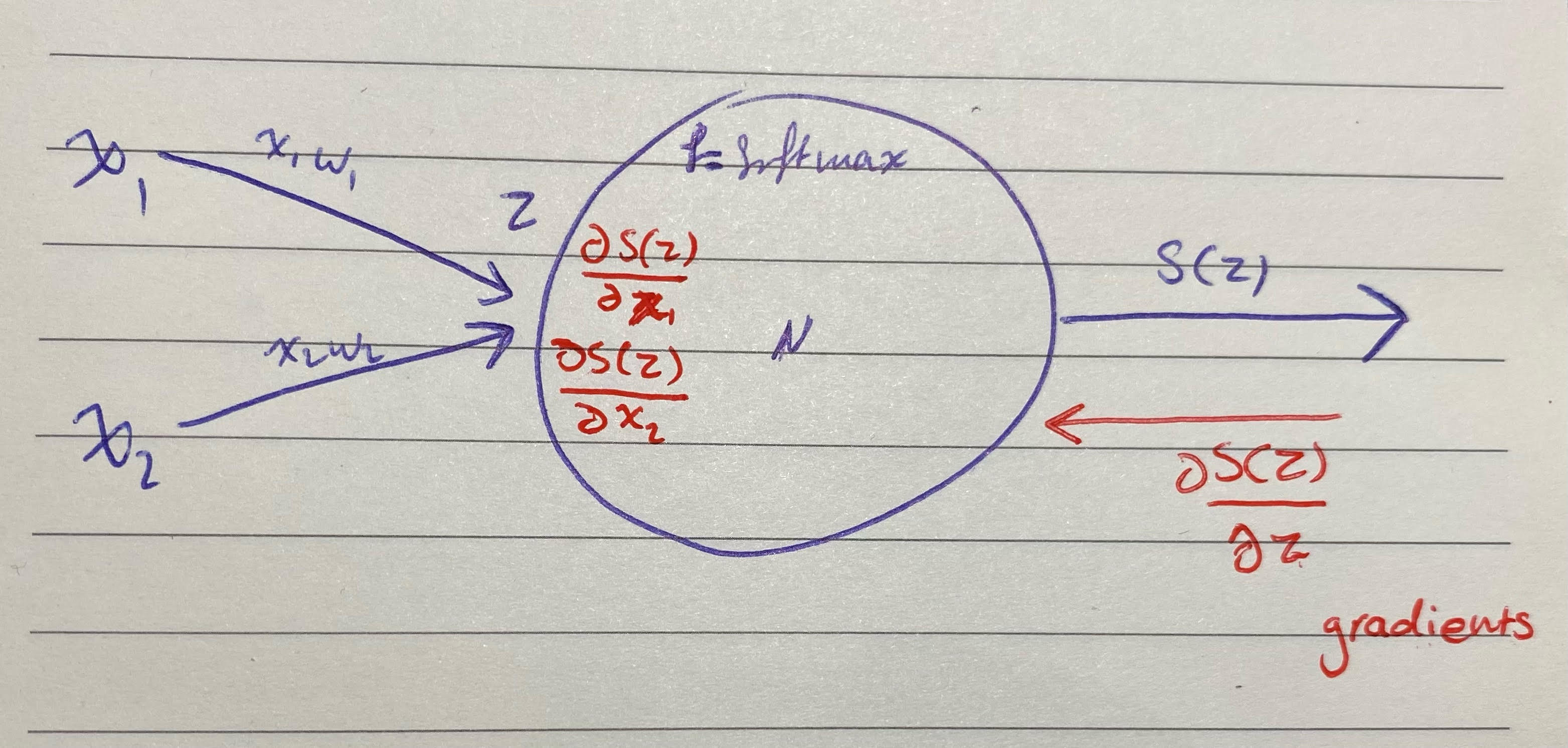
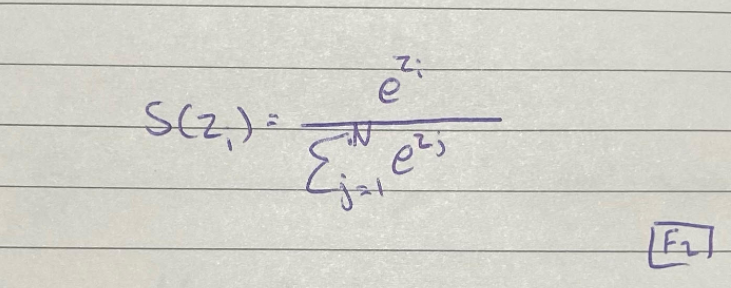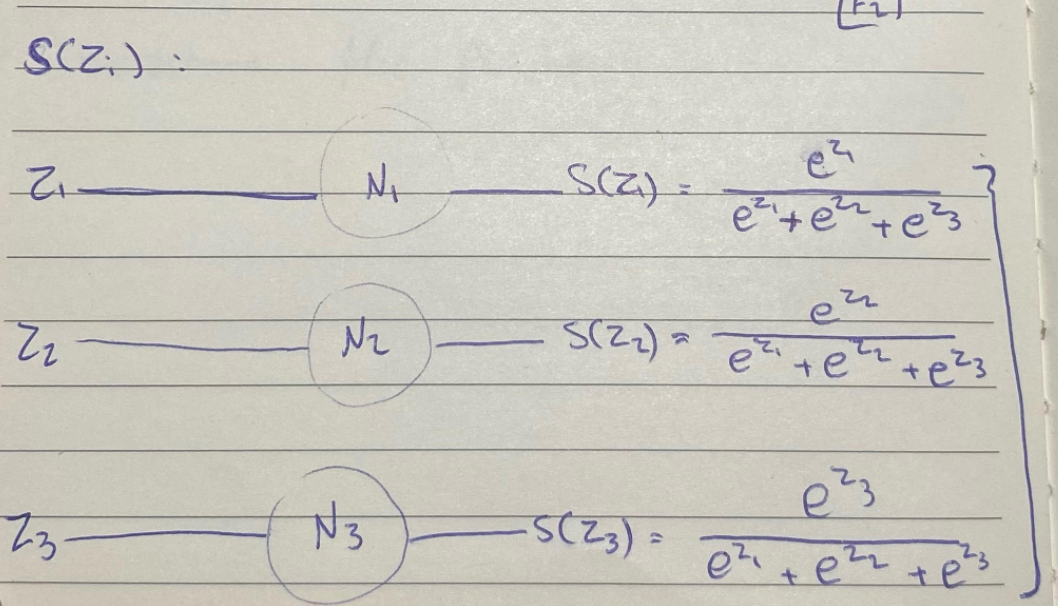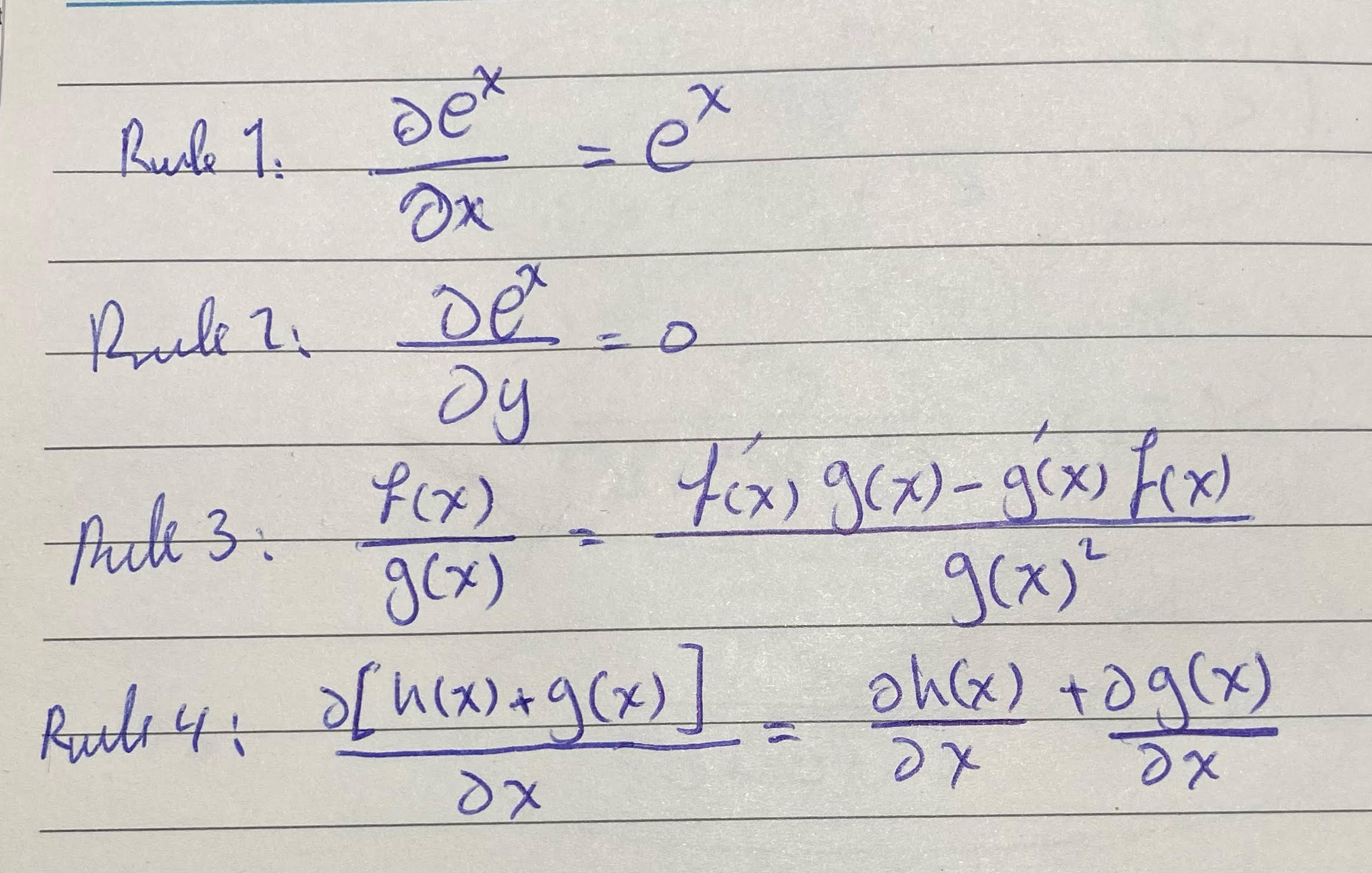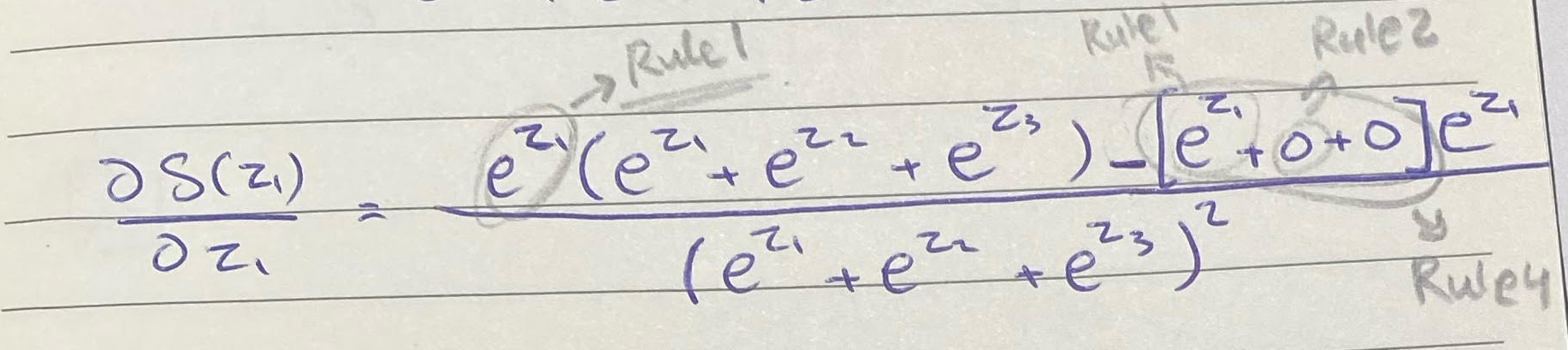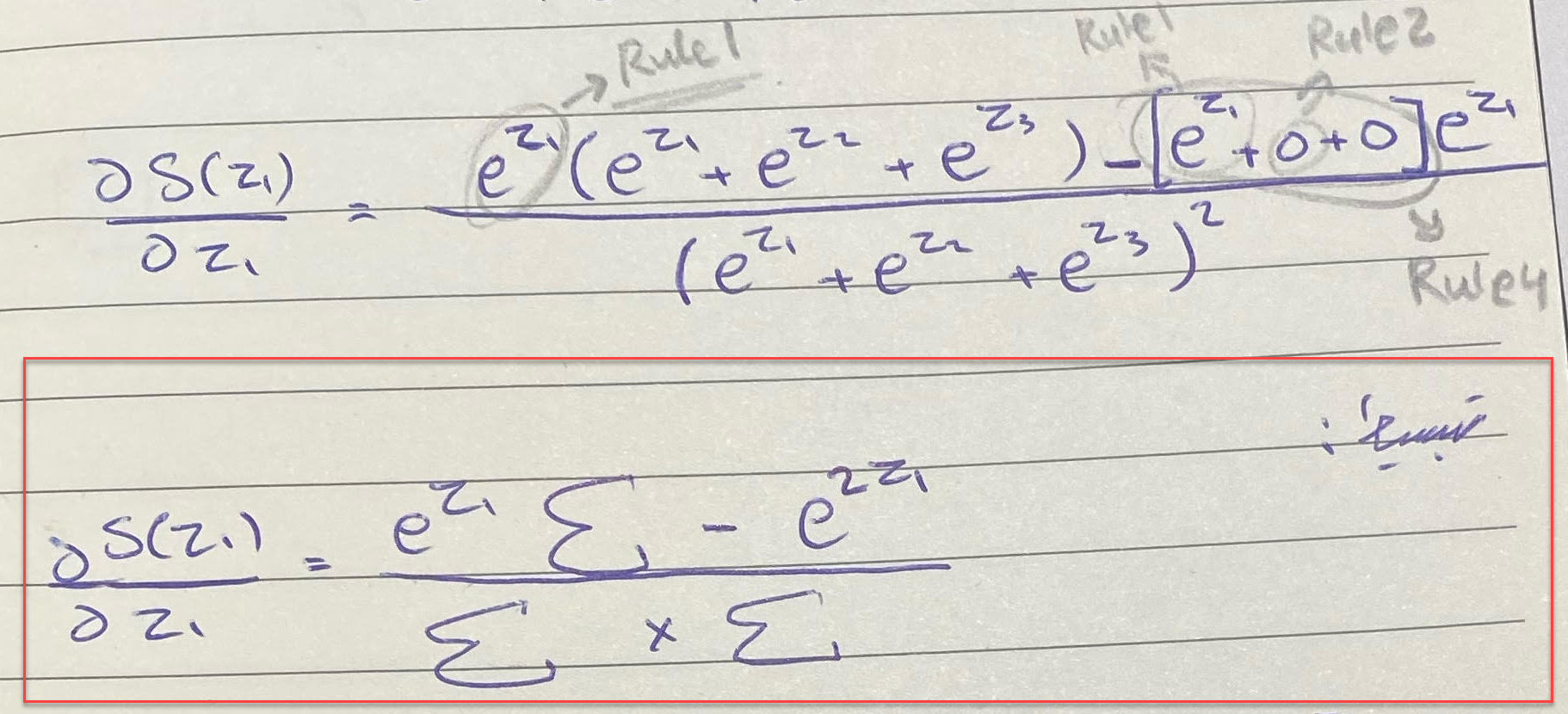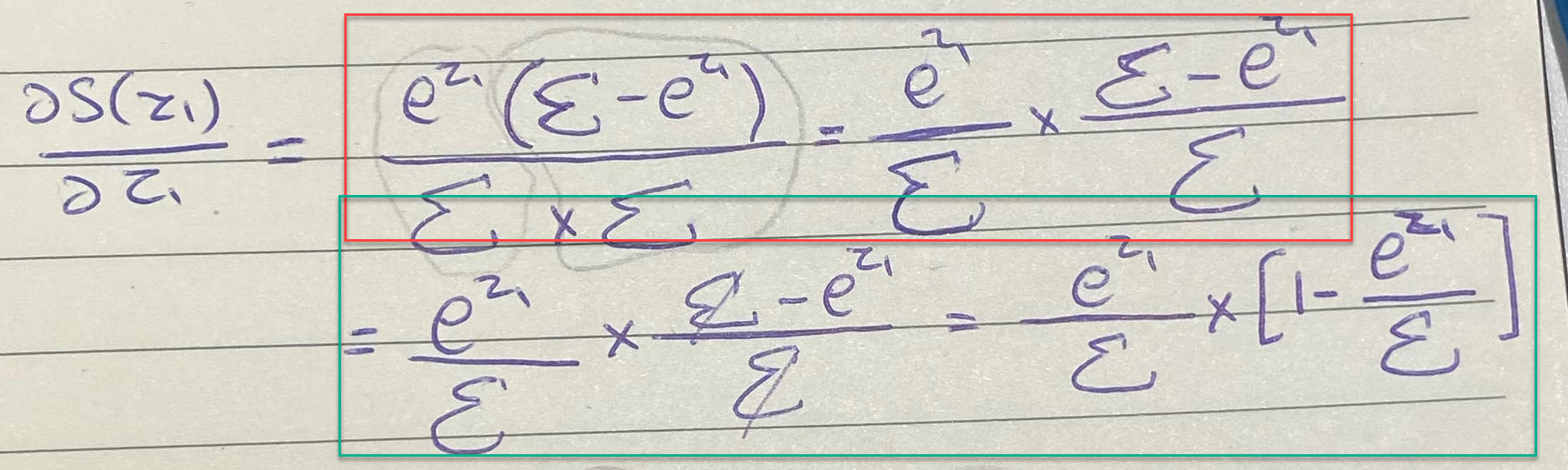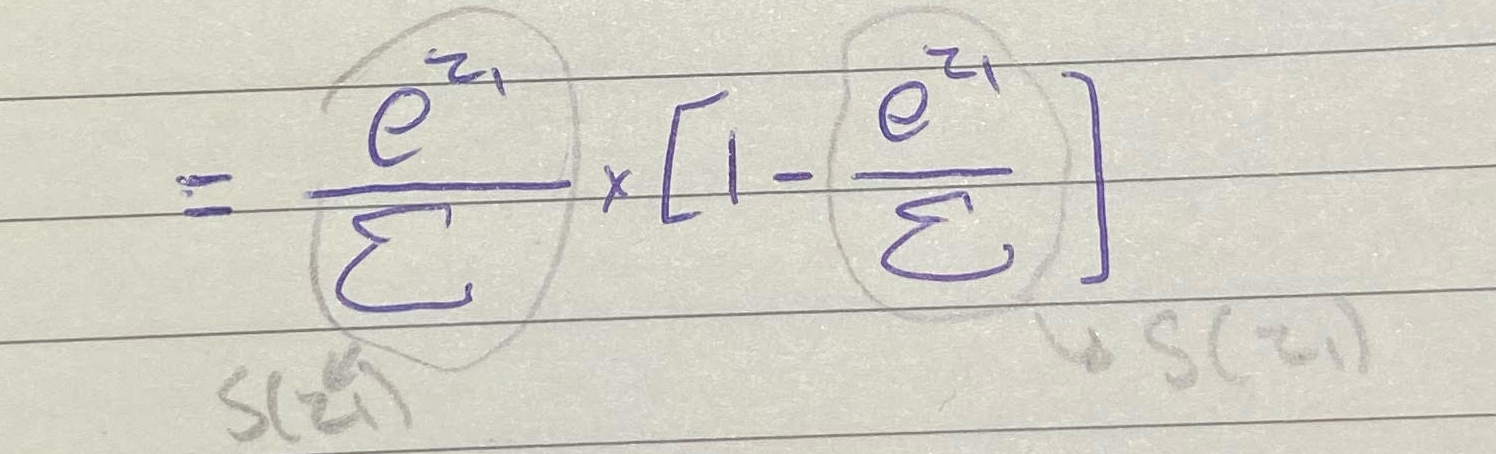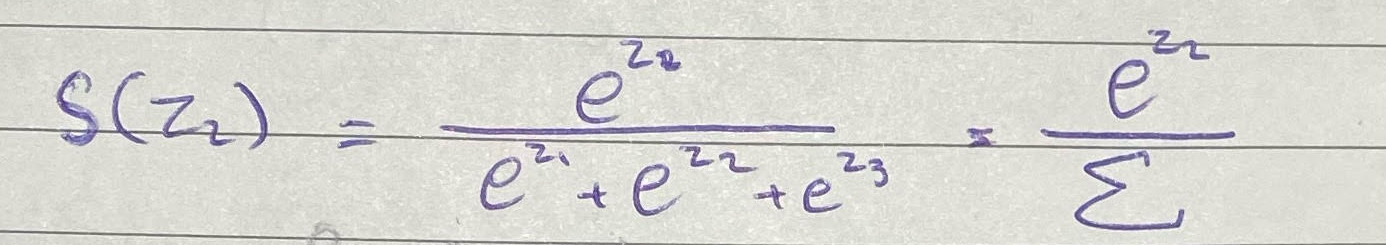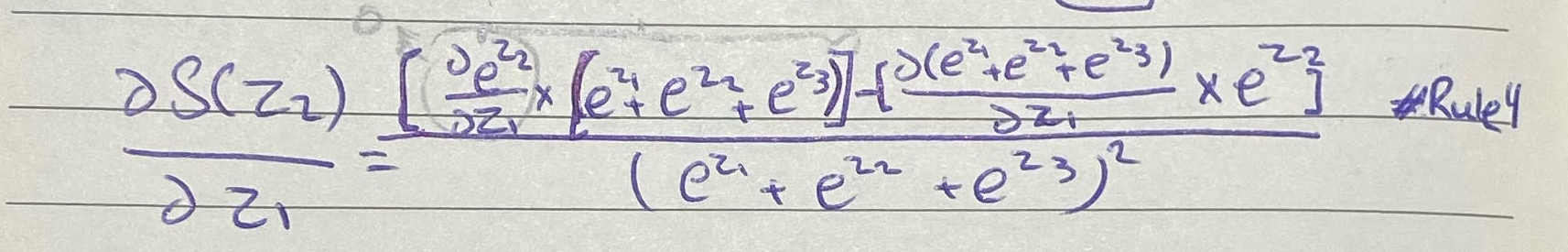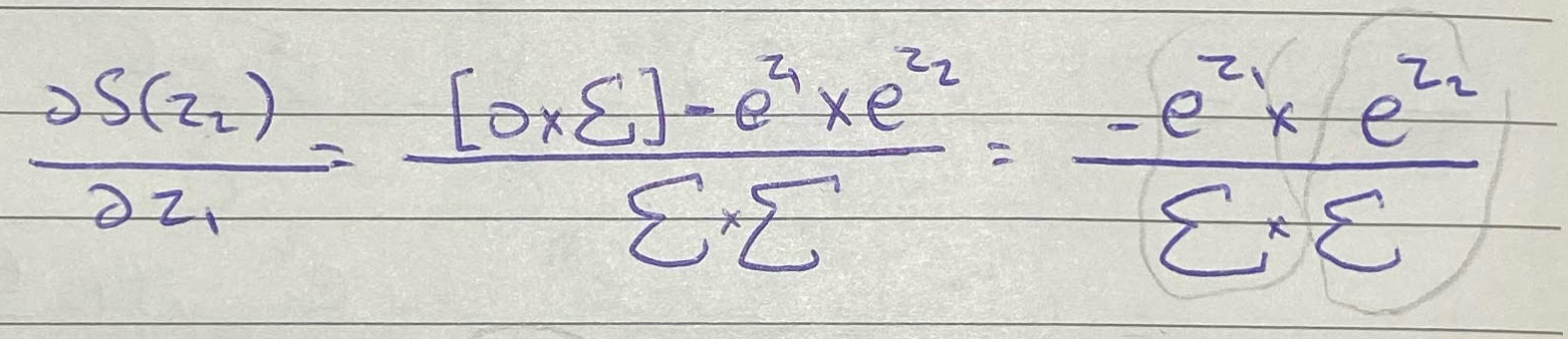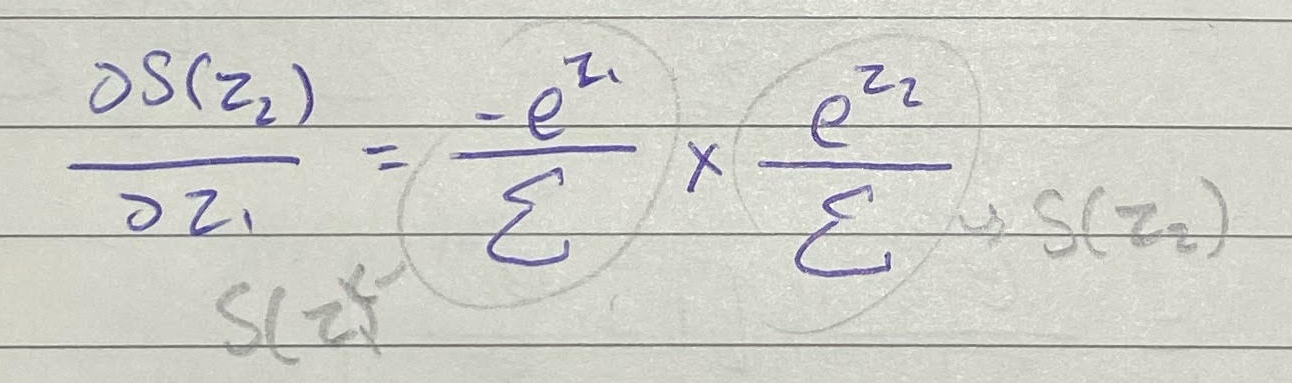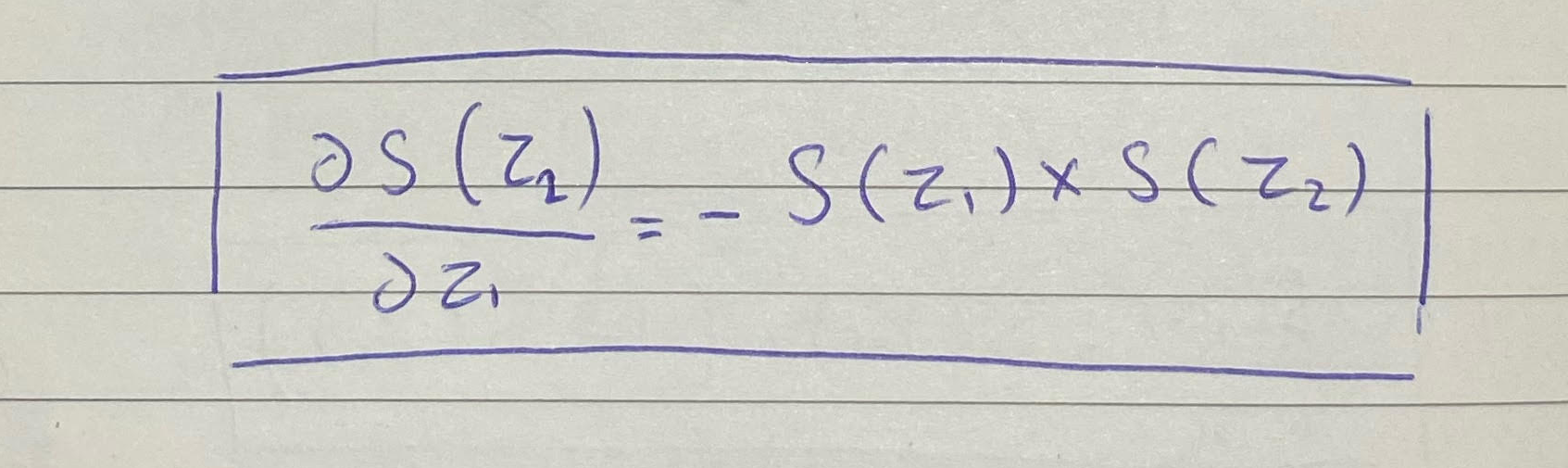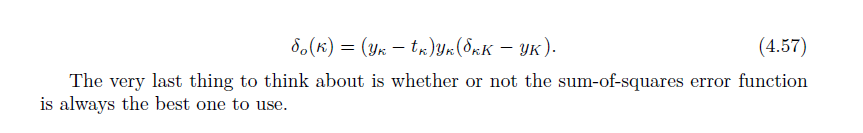احتاجت أحد صديقاتي مساعدة في فهم اشتقاق الـ SoftMax مما دفعني لإيضاح هذا المحتوى عربيًا ونشره لعموم الاستفادة.
أتوقع -وأتطلع- من القارئ الكريم في نهاية هذا المنشور أن يشتق الدالة بالنسبة لمتغير ولهذا أسهبت في ذكر بعض التفاصيل الأولية/البديهية لزيادة التثبيت وتعميق الفهم.
كما آمل من قارئ المنشور أن يكون مستقرًا في ذهنه بعض الأساسات عن التعلم العميق، ومبادئ الرياضيات و Neural Network
مقدمة
تعتبر SoftMax أحد activation function في مجال التعلم العميق، بالاطلاع على مجال الـ Neural Network نستطيع أن نستنتج أن دالة SoftMax تستخدم كدالة احتمالات تدلنا على التصنيف (Class) المناسب لمدخلِ ما؛ فلو كان عندي -مثلًا- ثلاثة تصنيفات: أشجار، بحار، سيارات فإن استخدام الدالة في آخر طبقة من الشبكة العصبية يساعد على التعرف على التصنيف (Class) للصورة المدخلة.
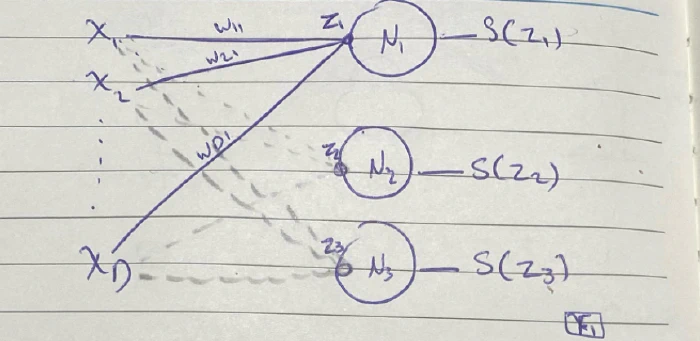
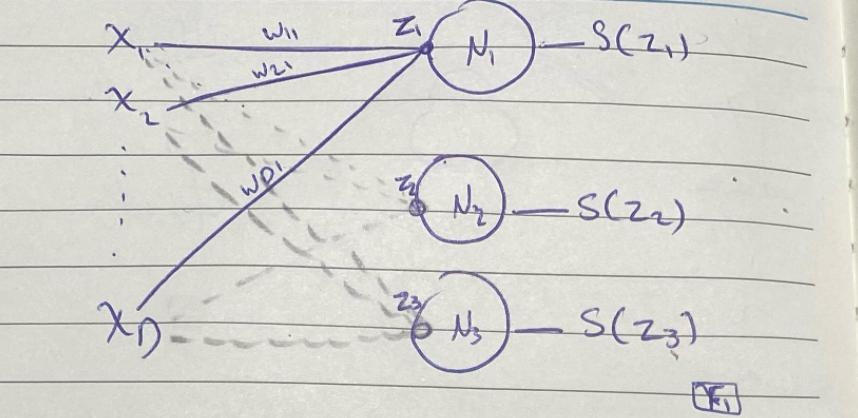
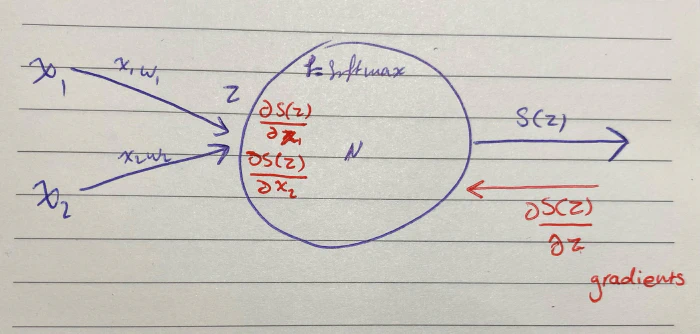
في الصورة مثال على NN بسيطة تحتوي على D من الأبعاد للمدخل، ثم (فلي كونكتد كونكشن) مع أوزانها، وأخيرًا مخرج واحد.
في حين أن طبقة المخرجات تحتوي على 3 خلايا عصبية فقط، فتكون دالة SoftMax للمدخل: مضروب (مجموع (مضروب الوزن والمدخل) ) + البايز
القانون رياضيا:
ماذا تمثل دالة الSoftMax ؟
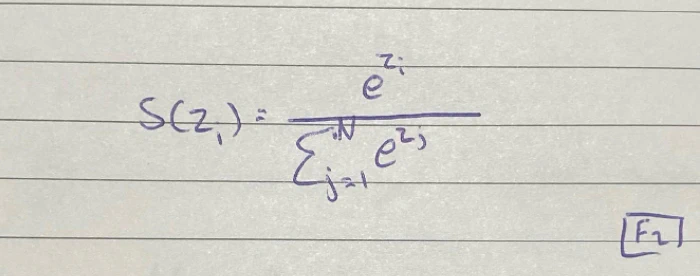
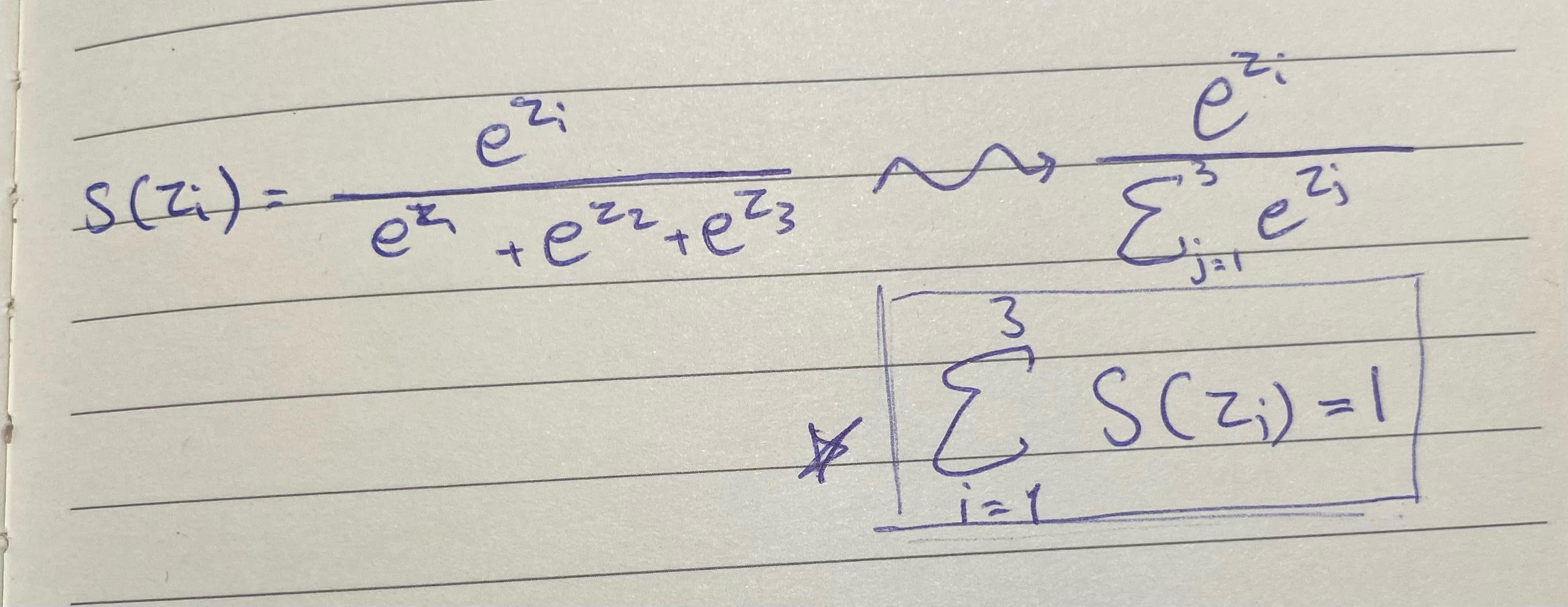
الملاحظ أن مخرج دالة SoftMax يمثل متجه، حيث S(Z) Arbitrary Vector ؛ فهي تحسب e المرفوع لقوة تساوي قيمة المدخل مقسومًا على مجموع e مرفوعة لقوة القيم الباقية.
حتى نستطيع استيعاب الدالة يجب أن نصطحب في أذهاننا أن:
دالة SoftMax هي دالة احتمالات، وهذا يعني بالضرورة أن مجموع i دائما = 1.
فلو رجعنا إلى الصورة F1 فسنجد أن لدينا 3 نتائج لـ Z ، وحسب مفهومنا لدالةSoftMax فإن مجموع نتائج الـ Z الثلاثة = 1
S(z1)+S(z2)+S(z3)=1
ملاحظة: هي ليست دالة احتمالات ولكن بإمكاننا استخدامها لقياس certainty في الNN حيث أنها تمتلك مزايا دوال الإحتمالات
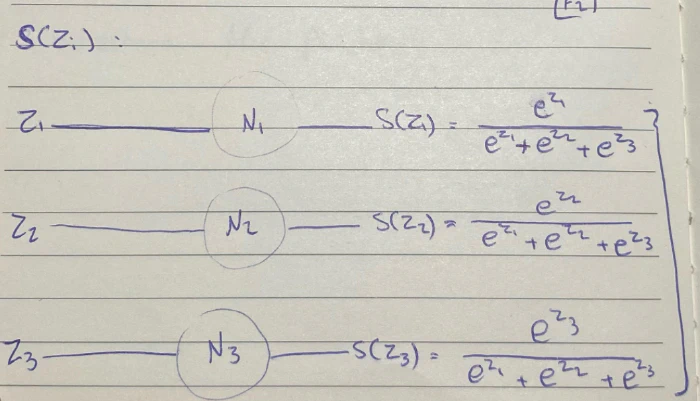
حيث يمكننا إعادة كتابتها بشكل مختصر و عام هكذا
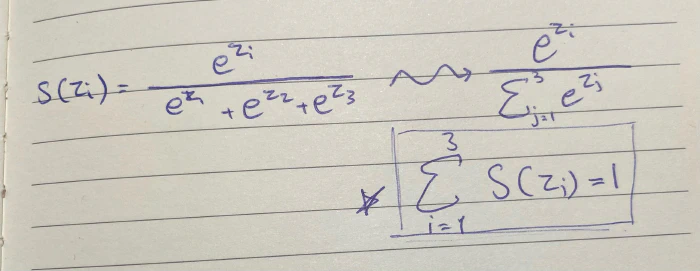
بعد توضيح الدالة ومعناها نستطيع أن نبدأ في اشتقاقها والذي قد يحتوي على بعض الخدع البسيطة التي تجعل عملية الاشتقاق عملية غير مباشرة.
بشكل مختصر جدًا
هدف السوفتماكس هي تحويل القيم الضخمة الى قيم بين 0 و 1، فالناتج من جمع هذه القيم يعطينا 1، بهذا يمكننا تحديد التصنيف الأقرب للمدخل
مشتقة سوفت ماكس بالنسبة لمتغير
مقدمة
كما يوضح التعبير الرياضي للدالة: أن المقام بين عناصر المتجه (Z) مشترك؛ مما يعني أن حساب الSoftMax لـ z1 سنضطر لحساب بقية عناصر المتجه (z1,z2,z3)
فهذا يعني يعني أنه من الضروري حساب المشتقة لهم جميعا S(Z1), S(Z2), S(Z3) بالنسبة لـ z1 وليس فقط S(Z1) بالنسبة لـ z1
لا بأس، سنتطرق للتفاصيل بشكل أكبر حتى تتضح
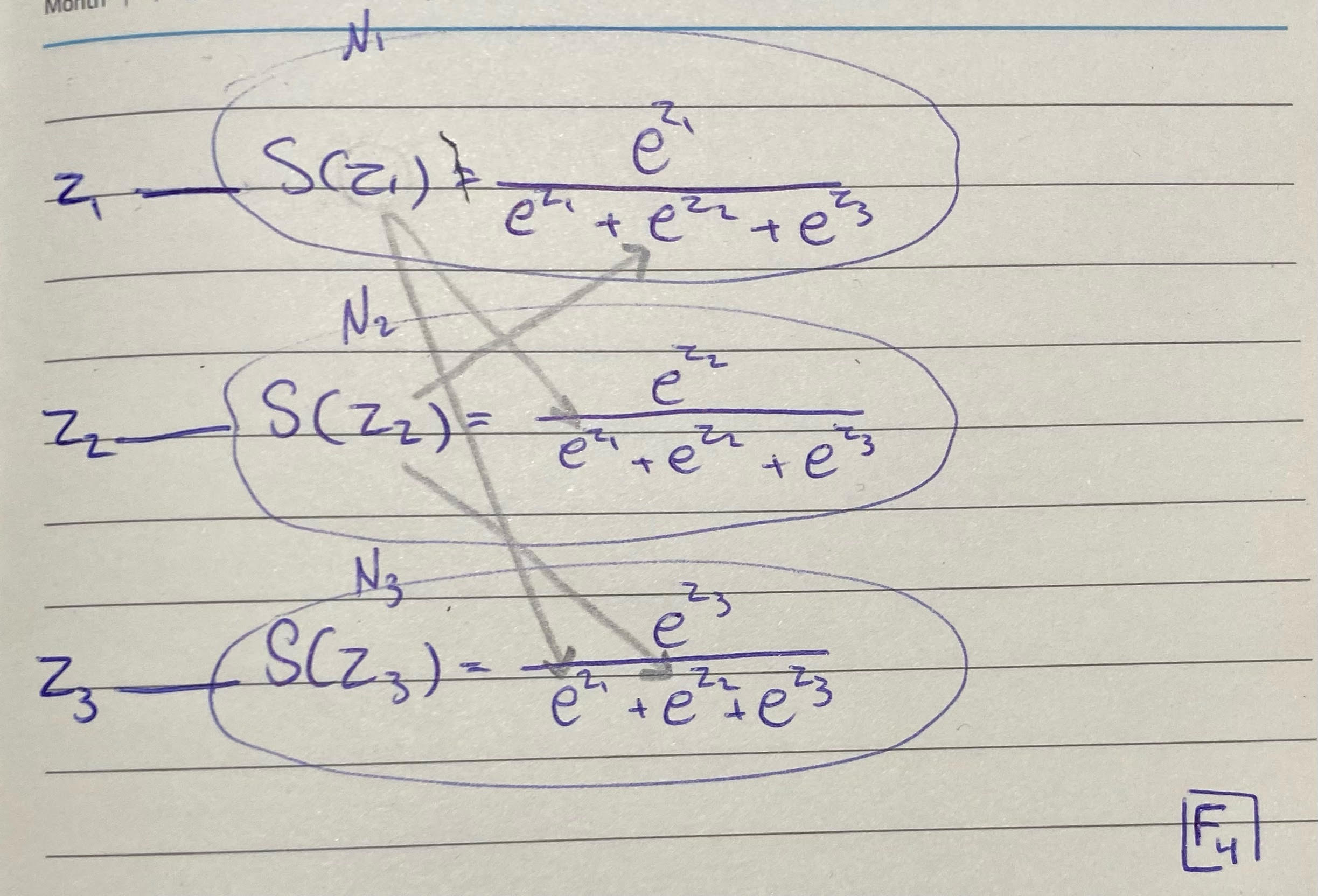
يتضح بالمثال أدناه العلاقات بين العناصر وبهذا تتضح الإعمادية
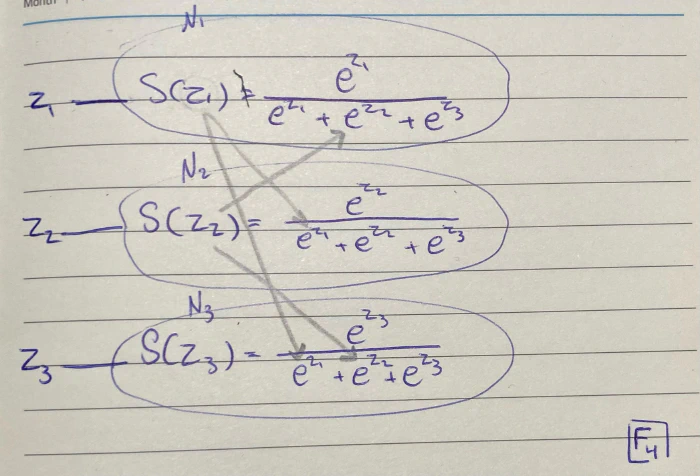
نجد أن S(z1) تعتمد على z2 و z2، وS(z2) تعتمد على z1 و z3، الآن دورك تكتشف S(z3) تعتمد على من؟
لذا مجددا عندما نريد حساب الاشتقاق الجزئي partial derivative للمتجه SoftMax بالنسبة للمدخل نحتاج نحسب الاشتقاق الجزئي partial derivative لكل العناصر بالنسبة لz1 وهو كذلك ل z2 و z2
إذا اعتبرنا Z متجه مكون من التالي
S(Z) = [ S(Z1), S(Z2), S(Z3) ]
إذا أردنا حساب الاشتقاق الجزئي partial derivative بالنسبة لمتغير واحد مثال:
$\frac{∂S(Z)}{∂z1}$
سوف نحتاج الى حساب $\frac{∂S(Z)}{∂z1}$ و $\frac{∂S(z2)}{∂z1}$ و $\frac{∂S(z3)}{∂z1}$.
يعود السبب لما هو واضح في F4 من اعتمادية بعضها على بعض، سنقوم بحسابها على حده حتى تتضح بشكل أفضل
الآن هو الجزء الممتع :)
قواعد أساسية
قبل لا نبدأ بالاشتقاق فيه عدد من القواعد الرياضية للاشتقاق يجب استحضارها وتذكرها حتى تكون العملية أسهل
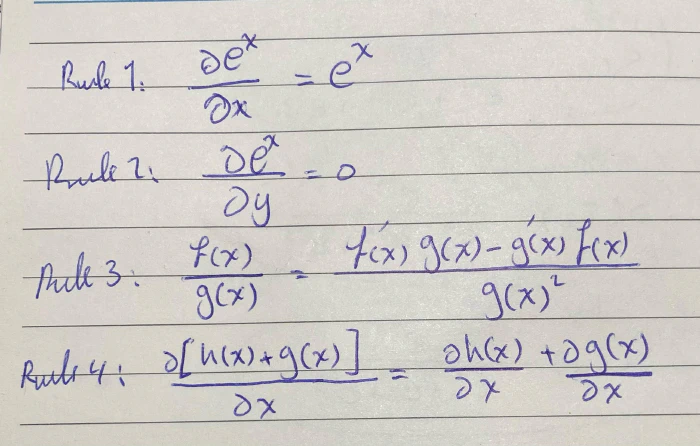
القاعدتين الأولى هي أشتقاق الأسي exponentials، الفرق بالقاعدة الأولى وهو بالنسبة لـ x والثانية بالنسبة إلى y يتضح بالثانية انها independente
القاعدة الثالثة هي مشتقةf(x)g(x) بالنسبة لـ x وهذه مشهورة جدًا وهي عبارة عن مضروب مشتقة f(x)فيg(x) مطروحة من مشتقة g(x) في f(x) على g(x) تربيع
القاعدة الأخيرة وهي مشتقة الجمع بالنسبة لمتغير، هو مجموع المشتقات كما موضح بالمثال أعلاه
الآن سنبدأ بإشتقاق دالة SoftMax لـ z1 بإننا نحللها خطوة خطوة
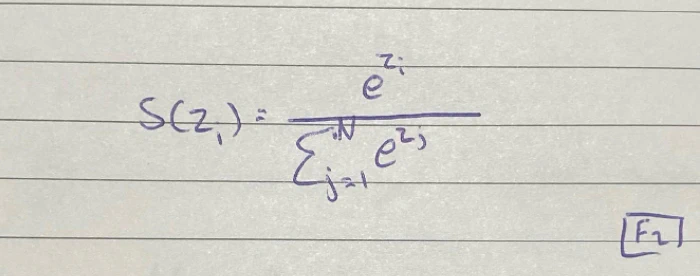
بالنسبة لدالة SoftMax ، كما نرى عبارة عن معادلة كسرية فالنقطة الأولى سوف نستخدم القاعدة الثالثة لبداية الإشتقاق
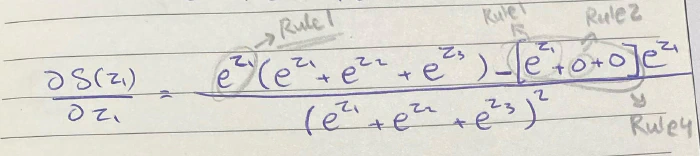
ستكون بهذا الشكل، لنفصل أكثر بداية اشتقاق f(x) وهي دالة أسية نستخدم معها القاعدة الأولى لذا ستبقى كما هي e^z1 بعدها g(x) كما هي، ثم نطرح هذه القيمة من f(x) وتبقى كما هي، ثم نضربها بمشتقة g(x)، وفي استخراج مشتقة g(x) متعة!
مشتقة g(x) عبارة عن مشتقة جمع القاعدة الرابعة، ومشتقة الجمع سيكون الاشتقاق الجزئي partial derivative للقيمة على الاشتقاق الجزئي partial derivative لـ z1
بتفصيل أكثر سوف تكون بهذا الشكل
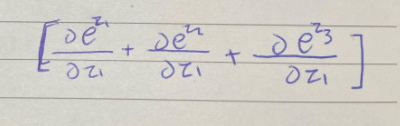
سنحتاج الى القاعدتين الأولى والثانية
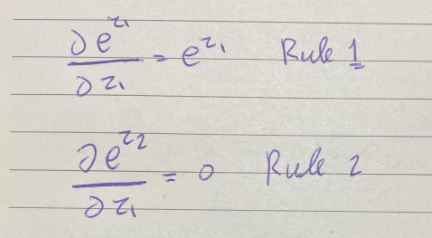
آخر حد $e^{z3}$، عليك ؛)
بالاخير سيكون لدينا الناتج عبارة عن $[e^{z1}+0+0]*e^{z1}$
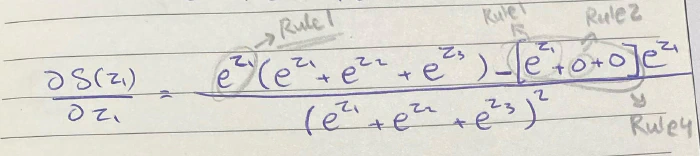
سنحاول تبسيط المسألة بطريقة مقروءة بشكل أفضل، لذا سنقوم بتبسيطين الأول فيما يتعلق بالحد الآخر بعد الطرح، والتبسيط الثاني فيما يتعلق بالمجموع.
بالنسبة للحد الثاني ما بعد الطرح بإمكاننا إعادة كتابته بهذا الشكل
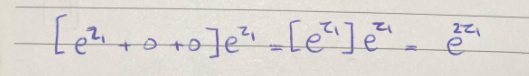
باستخدام خواص الضرب الأسي سيكون لدينا e^2z1
وبالنسبة للمجموع نحن نعرف أنه بإمكاننا استخدام علامة المجموع (summation symbol) Σ بدل كتابة (e^z1+e^z2+e^z3)، بشكل أوضح نطبقها على دالة SoftMax
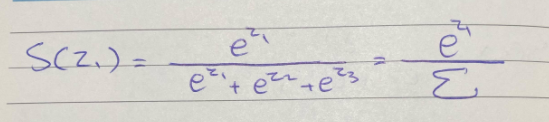
لذا سيكون الشكل النهائي للمعادلة بعد التبسيط هو:
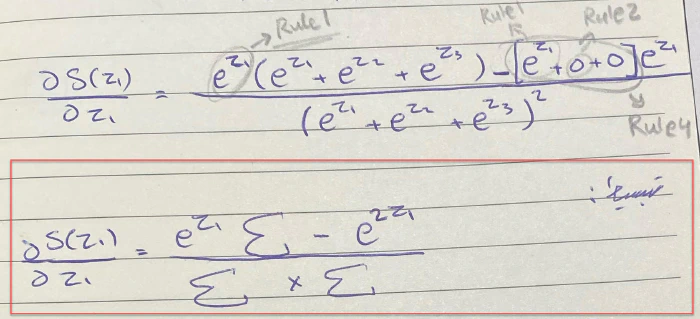
بالنسبة للبسط عملية بسيطة فناتج $e^zΣ-e^2z$ هو $e^{z1}(Σ-e^z1)$ سيكون شكل المعادلة الآن هكذا:
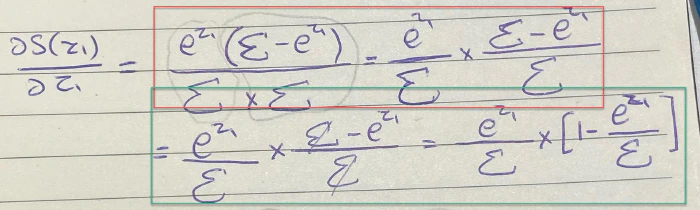
بالمستطيل الأحمر فقط قمنا بإعادة كتابتها بشكل يسهل علينا التعامل معها، بعد ما فصلناهما أصبحت العملية الحسابية أسهل، الآن بإمكاننا قسمة الحد على Σ وسيبقى لدينا [$1-\frac{e^z1}{Σ}$]
أصبح شكل المعادلة الآن مألوف لدينا، أرجعوا إلى تبسيطنا لمعادلة SoftMax عند F11 !
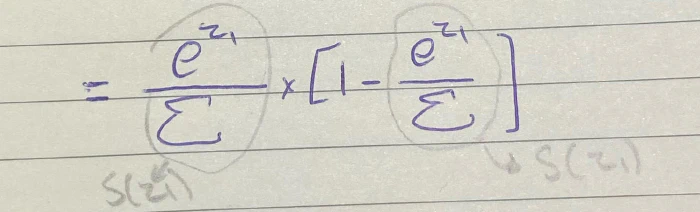
صحيح! أنهما عبارة عن دالة SoftMax لـ z1!
💥 لذا بالآخير بإمكاننا إستنتاج أن مشتقة S(z1) بالنسبة لـ z1 = $S(z1)*(1-S(1))$ !
الإشتقاق كاملًا هنا:

هذا كان S(z1) بالنسبة لـ z1، الآن بنحسب S(z2) بالنسبة لـ z1، بيكون أسهل مع تغير طفيف جدًا
بالبداية نحسبSoftMax لـ z2
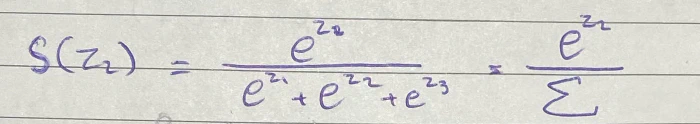
ولإشتقاقها بالنسبة لـ z1 نبدأ بنفس الخطوات السابقة بستخدام القاعدة الرابعة
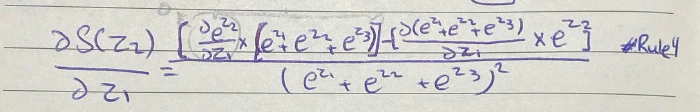
التغير البسيط سوف يكون على الطرف الأول حيث حساب مشتقة f(x) وهي e^z2 بالنسبة لـ z1 سيكون صفر أستخدامًا للقاعدة الثانية، والطرف الآخر مشابهه للإشتقاق الماضي
لتبسيط شكل المعادلة وإعادة كتابتها بشكل أوضح ستكون بهذا الشكل:
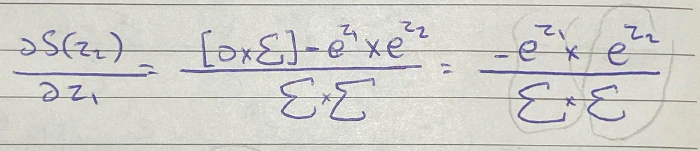
سيلغي الجزء الأول نفسه بما أنه مضروب بصفر، ثم سنعيد قسم المعادلة حتى يسهل التعامل معها مجددًا
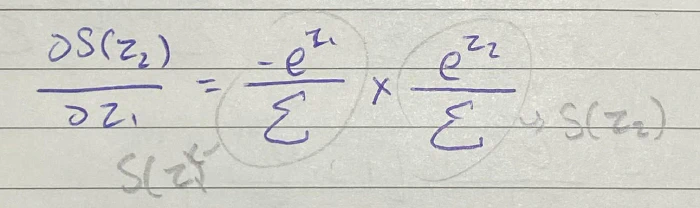
أصبح شكل الطرفين مألوف لدينا فالطرف الأول هو عبارة عن S(Z1) والطرف الآخر هو S(Z2) !
لذا يمكننا استنتاج أن اشتقاق S(z2) بالنسبة لـ z1 يساوي
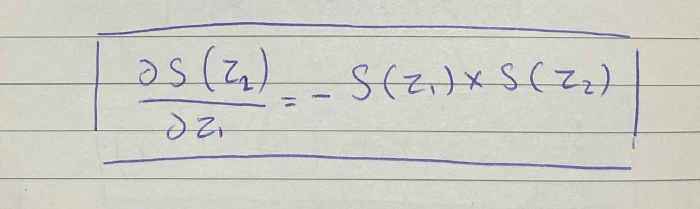
الخطوات كاملة هنا:

قم بإشتقاق S(z3) بالنسبة لـ z1 ثم عد للمقالة 😊
الإستنتاج
بعضكم بإمكانه إستنتاج بإنه لا داعي لإعادة الطريقة فبإمكاننا إستنتاج أن ناتج الإشتقاق سيكون $-S(z1)*S(z3)$، صحيح!
وهكذا على جميع المتغيرات الأخرى إن وجد، من هذا بإمكاننا أستنتاج أن هنالك حالتين لإشتقاق إذا كان المتغير المشتق i يساوي المشتق إليه j بمعنا أوضح i=j فأن النتيجة دائمًا ستكون $S(zi)*(1-S(zi))$ وإن كانا لا يتساويان فإن النتيجة ستكون دائمًا $-S(zi)*S(zj)$
بشكل أوضح:
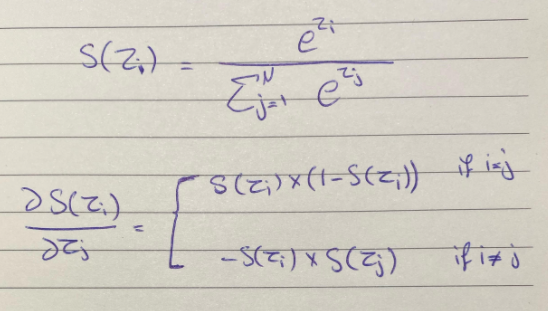
ونختم بعرض العملية كاملة لجمع الأفكار كلها
Code
def softmax(x):
exps = np.exp(x - x.max())
return exps / np.sum(exps)
def forward(self):
# self.input is a vector, and is the output of (w * x) + b
self.value = self.softmax(self.input)
def backward(self):
for i in range(len(self.value)):
for j in range(len(self.input)):
if i == j:
self.gradient[i,j] = self.value[i] * (1-self.value[i])
else:
self.gradient[i,j] = -self.value[i] * self.value[j]
المصادر:

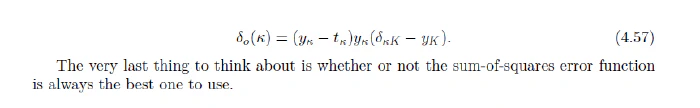
📕 MACHINE LEARNING An Algorithmic Perspective [Second Edition]
📰 Softmax classifier-CS231 Stanford University